IndexType： B+Tree

前言

今天要來介紹 B+Tree，B+Tree 是許多 db 的預設 index type，
甚至是 primary key 的預設 index type，無法更改。
為什麼 B+Tree 會這麼強大?
在這之前將介紹比較搜尋演算法的地板，
然後介紹 B Tree 的資料結構，最後演進至 B+Tree。

比較搜尋演算法的地板 Ω(log n)

我們來先看看這一個類似Binary Decision tree的東西。

有數值4，5，11被插入到這顆tree內，
internel node會做大小比較，leaf node為我們要找的數值。
像是root就是比5小的就走左邊，比11大的就走右邊，
所以如果要找5那麼就會經過5<的右邊和11<的左邊。

先宣告整棵樹的高為h，有n個value會被插入到這顆tree中。

h: height
n: value

我們可以這樣說，

1. 使用者想要search的值， 為n個數值中的其中一個，那麼有n個可能。

2. 使用者想要使用Binary Decision tree來search值，為leaf node中的其中一個，那麼binary tree leaf node有 2^(h-1)個可能。

3. 而當Binary Decision Tree不是perfect binary tree(各層節點全滿)時， 2^(h-1)>=n

所以我們得出一個不等式2^(h-1)>=n。

1. 兩邊取log2 h-1>=log2(n)
2. 忽略常數 h>=log2(n)

得出 h=Ω(log n)，

而h其實就是我們在Binary Decision Tree中做比較的次數。
所以我們可以得知，若是以比較搜尋法來說Lower Bound為Ω(log n)，
換句話說，搜尋一筆數值，至少需要花log n的時間複雜度，沒有比他更少的。

在 layer 動手腳

看到上面的證明後，得知地板就是 log n，
因此 tree 的 layer 會是一個重點，
如果 tree 長得歪斜，就會需要更多次的比較，
因此必須選用 Balanced Binary Tree，
讓 layer 盡量地保持平衡，每個 node 的比較次數就會趨於一致，
比較有名的 Balanced Binary Tree 為 AVL tree，
因不算主要重點，這裡不多作介紹。

在 degree 動手腳

得知地板就是 logm(n)，
如果想要再更加優化，那麼可以動手腳的地方就在於底數的 m，
調整每個 node 上可代表的值的個數，就能夠減少層數，並且增加 m 對於 n 的影響。
因此 M-way search trees 可以幫助我們優化 degree

資料結構

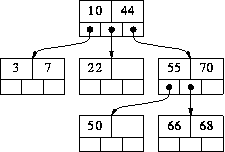
在介紹 B+Tree 資料結前，必須先介紹 B Tree，最後介紹 B+Tree。

B Tree

B Tree 其實就是一種個 M-way tree，
每一個內部節點只能有 2 或 3 個子節點，
換句話說 B Tree 其實就是 23 tree。

B+Tree

B+Tree 其實就是 B Tree 的進化，
B Tree 可以確保每個 node 的搜尋都是優化過的，
但如果要搜尋一個範圍 n 筆資料，
B Tree 就必須搜尋 n 次，
資料其實就在第一個找到的 node 的旁邊，
那麼我們就直接使用 pointer 的方式將 leaf node 連結起來，
這樣就可以達到搜尋一次，往下推多個的效果。

B+Tree 使用場景

做通用的單筆/範圍搜尋

B+tree in db

因 B+Tree 為預設的 index，所以不需要特別指定 index type
CREATE INDEX "{{INDEX_NAME}}" ON "{{TABLE_NAME}}" ({{COL_NAME}});
如果想要使用其他 index type 可以使用
CREATE INDEX "{{INDEX_NAME}}" ON "{{TABLE_NAME}}" USING "{{INDEX_TYPE}}" ({{COL_NAME}});

Remark: 各類 db 通常大同小異，這裡使用 postgres 作為範例

結語

在這個章節為了體會 index 的 default type 為什麼選用 b+tree，
介紹了比較搜尋演算法優化的最佳 bigO，
為了達到最佳 bigO ，使用 Balanced 與 m-way 做優化;
為了可以範圍搜尋，所以使用 b+tree;
可以說是最通用的 search algorithm，
因此許多 db 將 b+tree 作為 default type。
但通用歸通用，特殊情就還需依照特殊情境使用適當的 index type，
而非 b+tree 一路用到底，下面章節將會陸續介紹其他 index type。

參考資料

1. CH10. Multi-way Search Trees
2. PostgreSQL Index Types
3. Possible to use a BRIN Index on a Primary Key in PostgreSQL
4. AVL Tree Data Structure
5. BPlusTree
6. BTree
7. Introduction of B-Tree
8. File:PostgreSQL B-tree.svg
9. Sorting Lower Bound